Wireworld

Wireworld is a Turing-complete Cellular Automaton, first described by Brian Silverman in 1987. Wireworld can be used to simulate electronic gates, or logic elements.

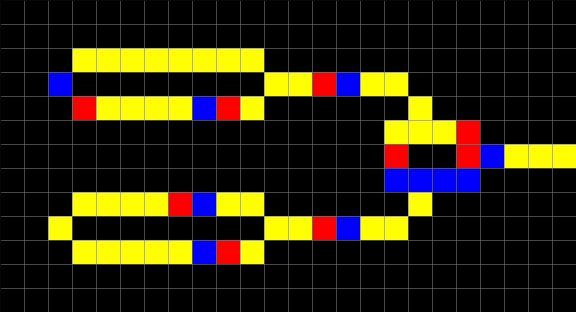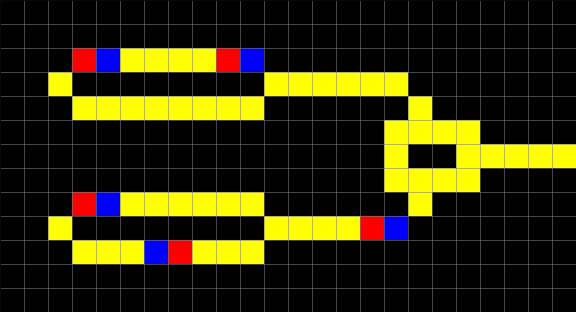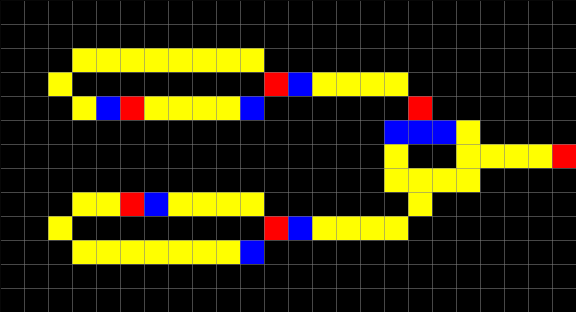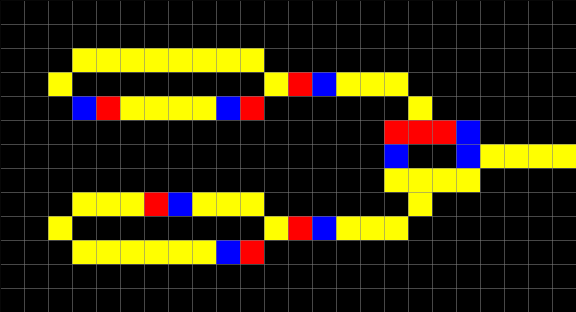
An example of Wireworld diodes, implemented with CellPyLib, is given below:

import cellpylib as cpl
import numpy as np
from matplotlib.colors import ListedColormap


def wireworld_rule(n, c, t):
    current_activity = n[1][1]
    if current_activity == 0:  # empty
        return 0
    if current_activity == 1:  # electron head
        return 2
    if current_activity == 2:  # electron tail
        return 3
    if current_activity == 3:  # conductor
        electron_head_count = np.count_nonzero(n == 1)
        return 1 if electron_head_count == 1 or electron_head_count == 2 else 3


cellular_automata = np.array([[
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 3, 3, 0, 0, 0, 0, 0, 0],
    [2, 1, 3, 3, 3, 3, 3, 0, 3, 3, 3, 3, 3, 3],
    [0, 0, 0, 0, 0, 0, 3, 3, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 3, 3, 0, 0, 0, 0, 0, 0],
    [2, 1, 3, 3, 3, 3, 0, 3, 3, 3, 3, 3, 3, 3],
    [0, 0, 0, 0, 0, 0, 3, 3, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
]])

cellular_automata = cpl.evolve2d(cellular_automata, timesteps=15,
                                 apply_rule=wireworld_rule, neighbourhood="Moore")

cpl.plot2d_animate(cellular_automata, show_grid=True, show_margin=False, scale=0.3,
                   colormap=ListedColormap(["black", "blue", "red", "yellow"]))
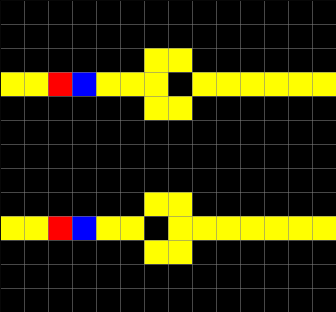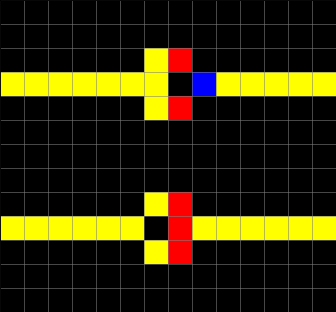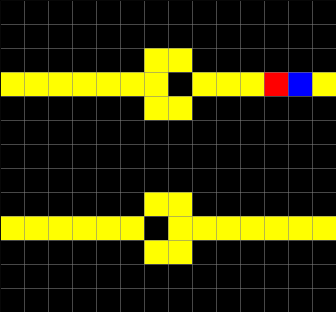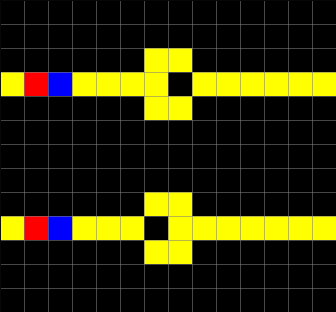
_images/wireworld_diodes.gif

An example of a Wireworld XOR gate, implemented with CellPyLib, gate is given below:

import cellpylib as cpl
import numpy as np
from matplotlib.colors import ListedColormap


def wireworld_rule(n, c, t):
    current_activity = n[1][1]
    if current_activity == 0:  # empty
        return 0
    if current_activity == 1:  # electron head
        return 2
    if current_activity == 2:  # electron tail
        return 3
    if current_activity == 3:  # conductor
        electron_head_count = np.count_nonzero(n == 1)
        return 1 if electron_head_count == 1 or electron_head_count == 2 else 3


cellular_automata = np.array([[
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 3, 3, 3, 3, 3, 3, 3, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 2, 1, 3, 3, 3, 3, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 3, 1, 2, 3, 3, 3, 3, 1, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 3, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3, 0, 0, 3, 3, 3, 3, 2],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3, 3, 3, 3, 0, 0, 0, 0],
    [0, 0, 0, 3, 3, 2, 1, 3, 3, 3, 3, 0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0],
    [0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 2, 1, 3, 3, 3, 3, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 3, 3, 3, 3, 3, 3, 3, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
]])

cellular_automata = cpl.evolve2d(cellular_automata, timesteps=25,
                                 apply_rule=wireworld_rule, neighbourhood="Moore")

cpl.plot2d_animate(cellular_automata, show_grid=True, show_margin=False, scale=0.3,
                   colormap=ListedColormap(["black", "blue", "red", "yellow"]))
_images/wireworld_xor.gif

References:

https://en.wikipedia.org/wiki/Wireworld

Dewdney, A K (January 1990). “Computer recreations: The cellular automata programs that create Wireworld, Rugworld and other diversions”. Scientific American. 262 (1): 146–149.