Two-Dimensional CA

CellPyLib supports 2-dimensional cellular automata with periodic boundary conditions. The number of states, k, can be any whole number. The neighbourhood radius, r, can also be any whole number, and both Moore and von Neumann neighbourhood types are supported. The following snippet demonstrates creating a 2D totalistic cellular automaton:

import cellpylib as cpl

# initialize a 60x60 2D cellular automaton
cellular_automaton = cpl.init_simple2d(60, 60)

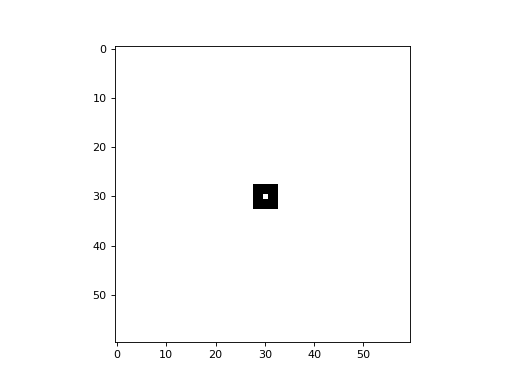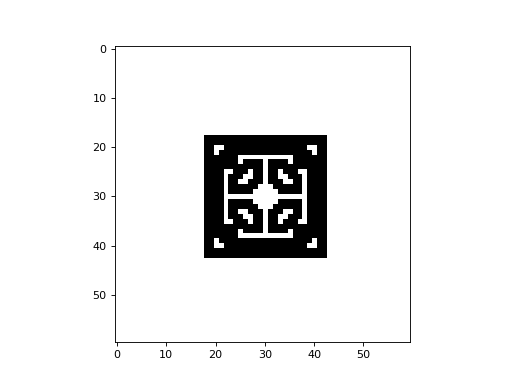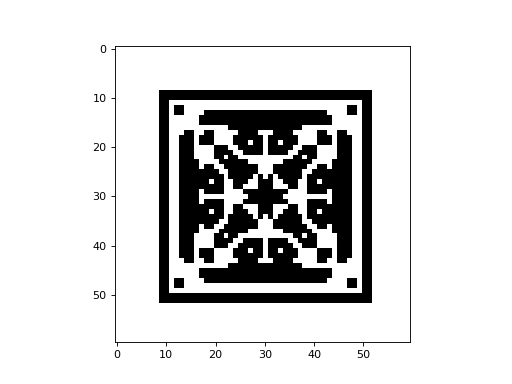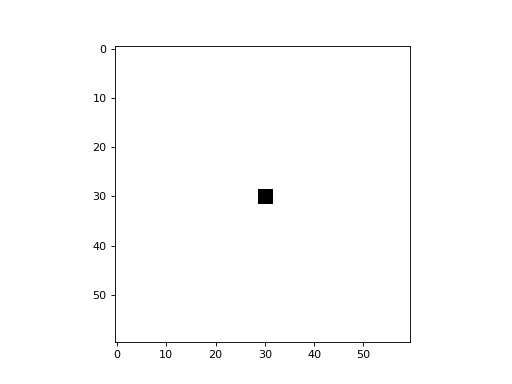
# evolve the cellular automaton for 30 time steps,
#  applying totalistic rule 126 to each cell with a Moore neighbourhood
cellular_automaton = cpl.evolve2d(cellular_automaton, timesteps=30, neighbourhood='Moore',
                                  apply_rule=lambda n, c, t: cpl.totalistic_rule(n, k=2, rule=126))

cpl.plot2d(cellular_automaton)

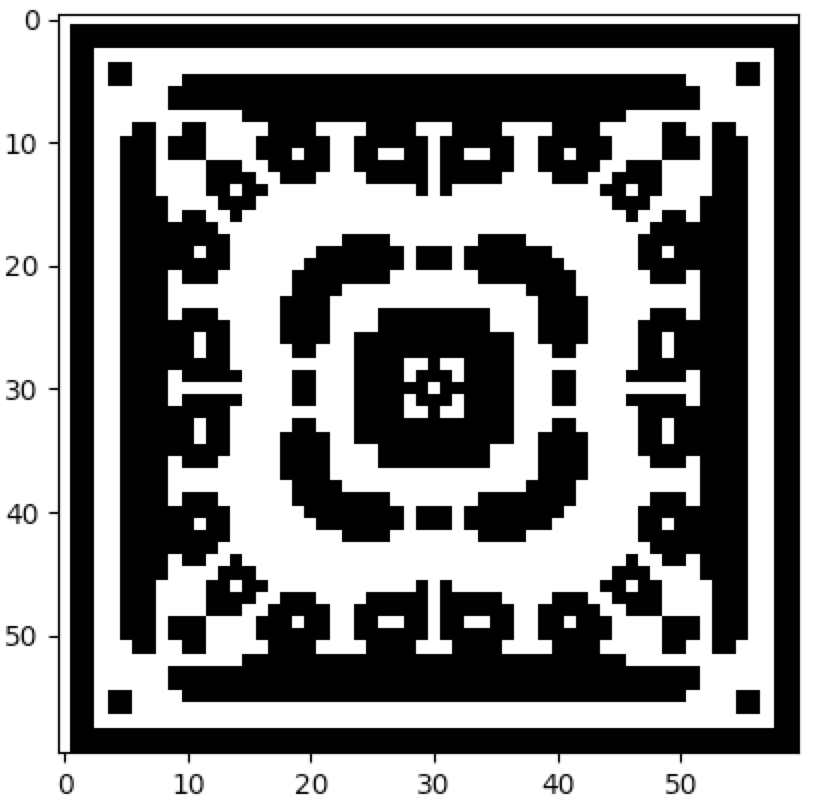
The image above represents the state at the final timestep. However, the state of the CA at any timestep can be visualized using the plot2d timestep argument. For example, in the code snippet below, the state at the 10th timestep is plotted:

cpl.plot2d(cellular_automaton, timestep=10)

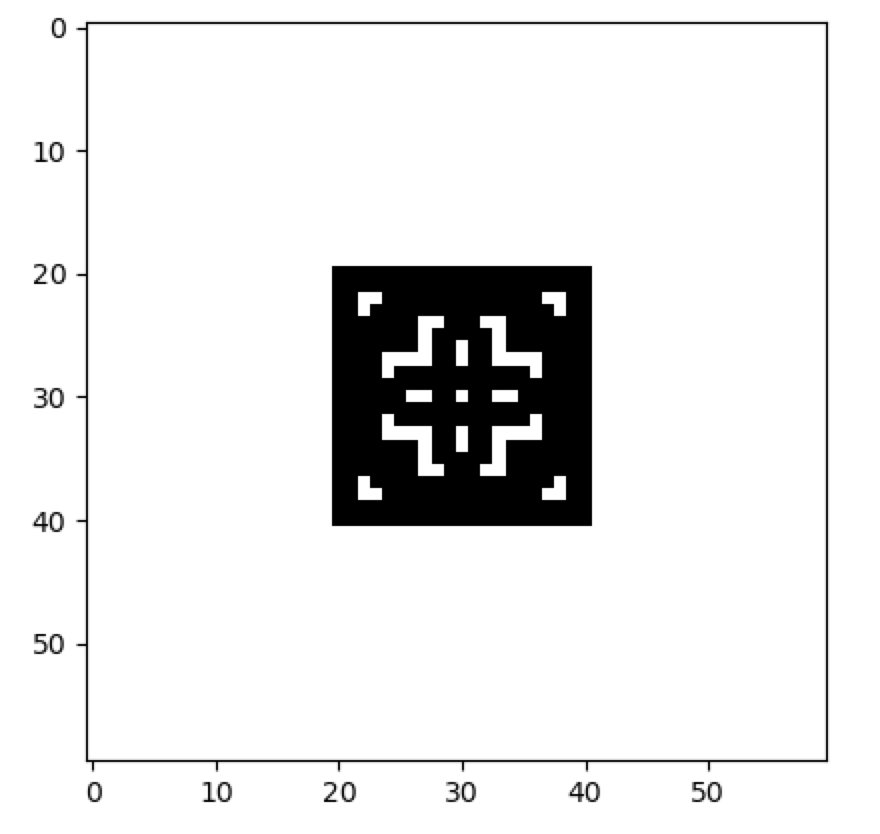
Note that 2D CA can also be animated, so that the entire evolution of the CA can be visualized, using the plot2d_animate function:

cpl.plot2d_animate(cellular_automaton)