Elementary CA
Elementary CA (ECA) were studied extensively by Stephen Wolfram in his book A New Kind of Science. These are perhaps the simplest kind of CA that one can conceive, with 2 states and a neighbourhood consisting of 3 cells (i.e. a radius of 1). There are a total of 256 ECA (i.e. there are 256 different ways of specifying a rule table for the 8 possible binary states of a neighbourhood). It is thus possible to exhaustively explore this space of discrete dynamical systems. As such, it is one of the most studied and well understood type of CA.
CellPyLib supports the creation of ECA through the nks_rule() function. This function
accepts as a parameter the rule number, using the convention introduced by Stephen Wolfram in his book A New Kind of
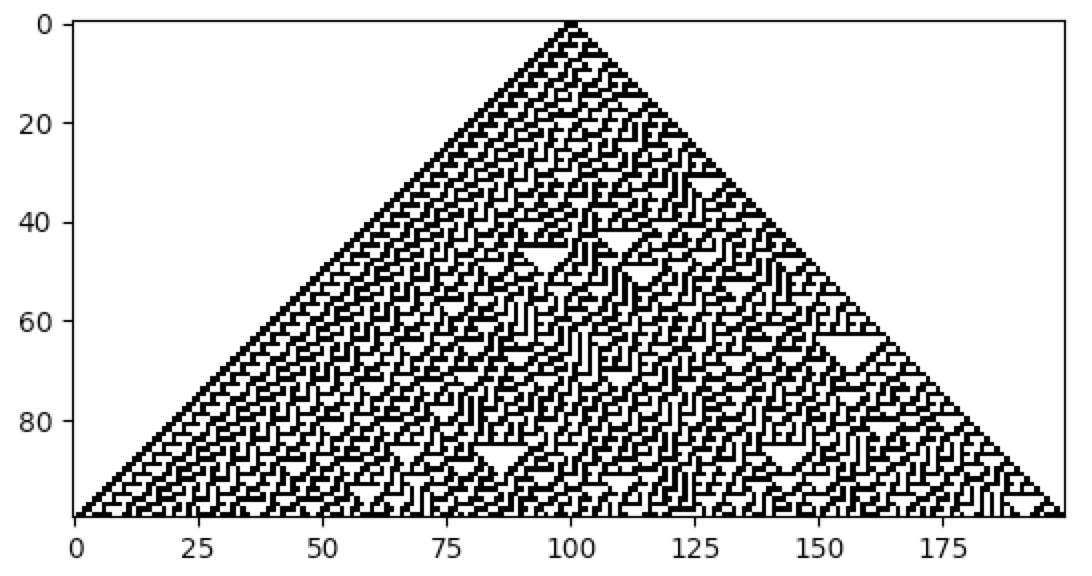
Science. The rule number uniquely identifies an ECA. For example, Rule 30 is a famous ECA. Its behaviour is very
complex, and it remains poorly understood. Questions regarding its evolution remain unanswered at the time of this
writing, and there is even a Rule 30 Prize, offered to those who can answer
fundamental questions about this fascinating dynamical system.
The following code snippet demonstrates creating and visualizing Rule 30 with CellPyLib:
import cellpylib as cpl
cellular_automaton = cpl.init_simple(200)
cellular_automaton = cpl.evolve(cellular_automaton, timesteps=100, memoize=True,
apply_rule=lambda n, c, t: cpl.nks_rule(n, 30))
cpl.plot(cellular_automaton)
Alternatively, the NKSRule class can be used:
cellular_automaton = cpl.evolve(cellular_automaton, timesteps=100, memoize=True,
apply_rule=cpl.NKSRule(30))
References:
Wolfram, S. (2002). A New Kind of Science. Champaign, IL: Wolfram Media.