Measures of Complexity

CellPyLib provides various built-in functions which can act as measures of complexity in the cellular automata being examined. These are the information-theoretic properties known as the Shannon entropy and mutual information, implemented in the average_cell_entropy() and average_mutual_information() functions.

Average Cell Entropy

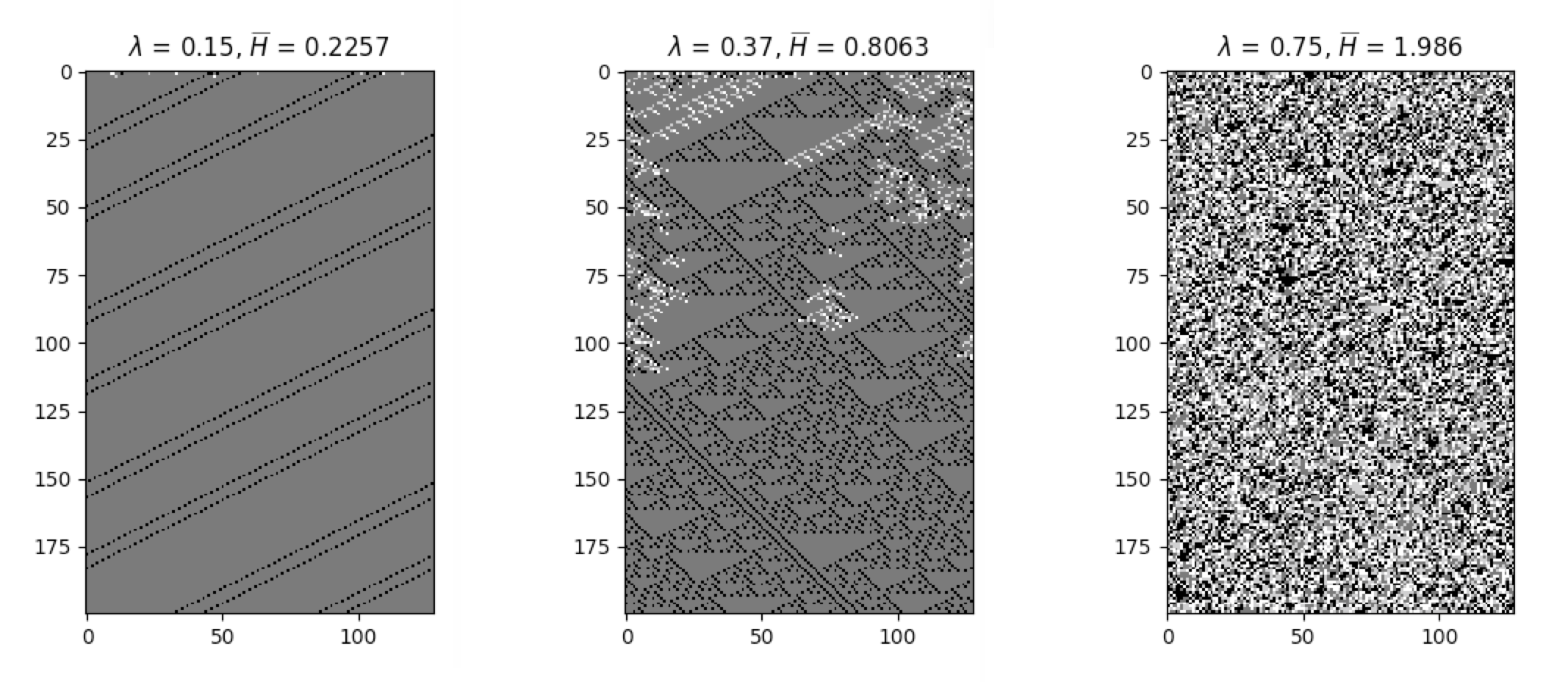
Average cell entropy can reveal something about the presence of information within cellular automata dynamics. The built-in function average_cell_entropy() provides the average Shannon entropy per single cell in a given cellular automaton. The following snippet demonstrates the calculation of the average cell entropy:

import cellpylib as cpl

cellular_automaton = cpl.init_random(200)

cellular_automaton = cpl.evolve(cellular_automaton, timesteps=1000,
                                apply_rule=lambda n, c, t: cpl.nks_rule(n, 30))

# calculate the average cell entropy; the value will be ~0.999 in this case
avg_cell_entropy = cpl.average_cell_entropy(cellular_automaton)

The following plots illustrate how average cell entropy changes as a function of Langton’s lambda:

Average Mutual Information

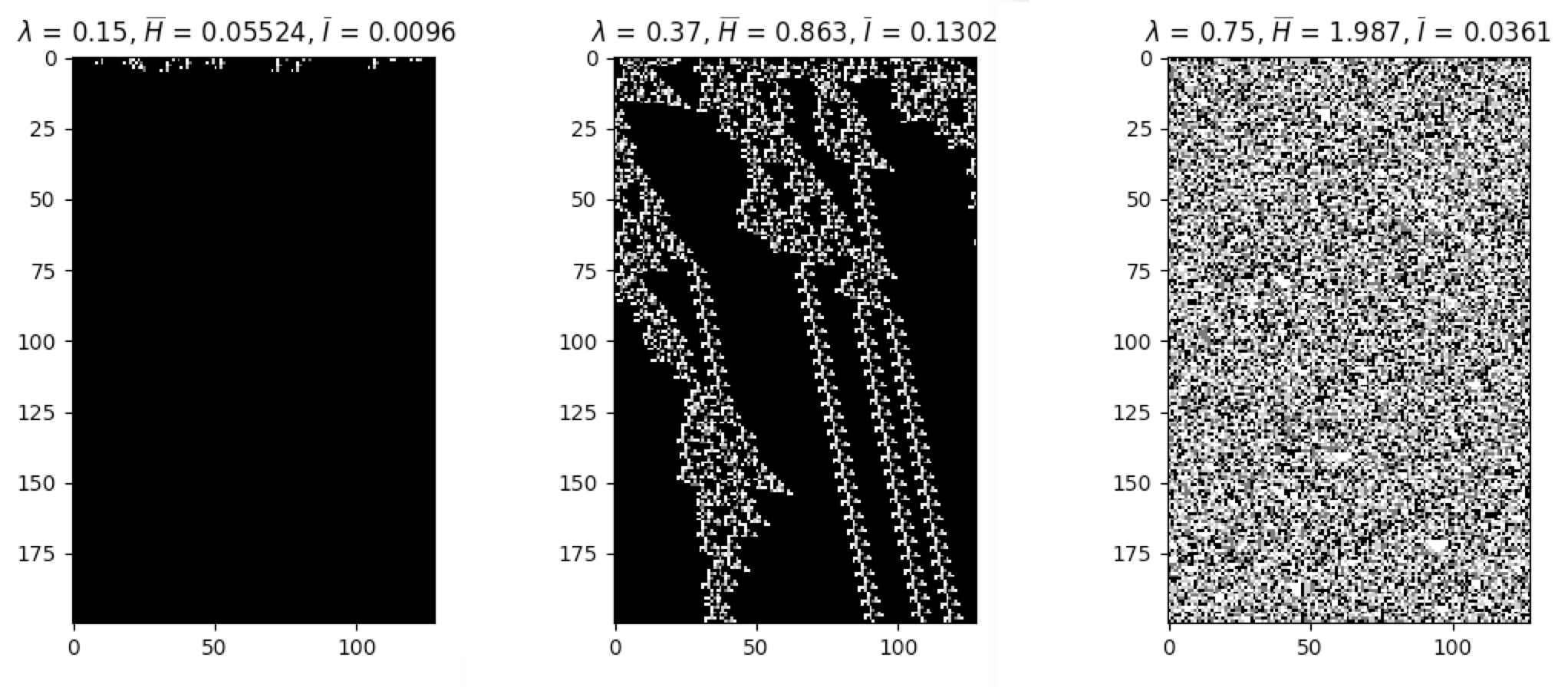
The degree to which a cell state is correlated to its state in the next time step can be described using mutual information. Ideal levels of correlation are required for effective processing of information. The built-in function average_mutual_information() provides the average mutual information between a cell and itself in the next time step (the temporal distance can be adjusted). The following snippet demonstrates the calculation of the average mutual information:

import cellpylib as cpl

cellular_automaton = cpl.init_random(200)

cellular_automaton = cpl.evolve(cellular_automaton, timesteps=1000,
                                apply_rule=lambda n, c, t: cpl.nks_rule(n, 30))

# calculate the average mutual information between a cell and itself in the next time step
avg_mutual_information = cpl.average_mutual_information(cellular_automaton)

The following plots illustrate how average mutual information changes as a function of Langton’s lambda:

References

Langton, C. G. (1990). Computation at the edge of chaos: phase transitions and emergent computation. Physica D: Nonlinear Phenomena, 42(1-3), 12-37.