Fredkin’s Self-Replicating CA

Ed Fredkin described an interesting cellular automaton that exhibits self-replication. The CA is 2-dimensional, and can consist of two or more colors. To compute the state of a cell at the next timestep, one sums the states of the neighbouring cells, modulo p, where p represents the number of colors. The neighborhood can be either of the Moore or von Neumann type. As the CA evolves, copies of the initial configuration will be produced. The examples below of these CA are based on John D. Cook’s blog posts, here and here:

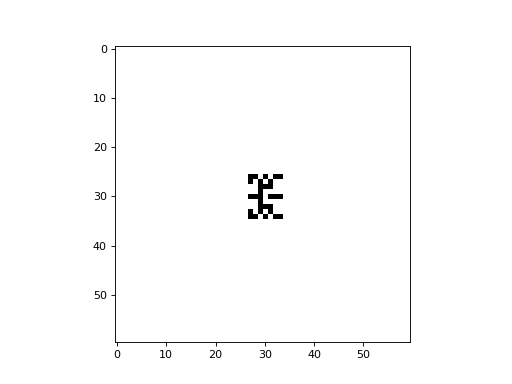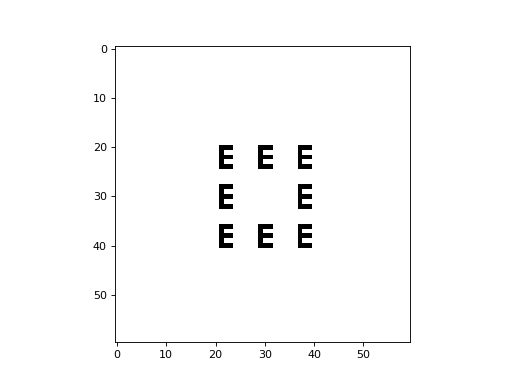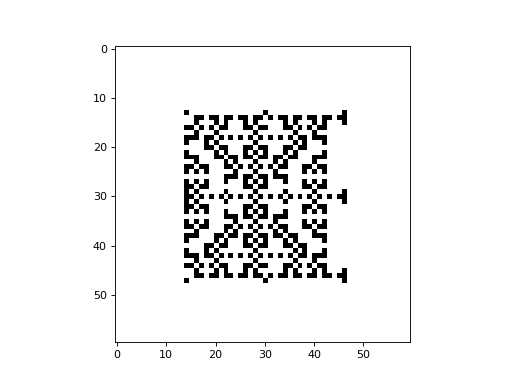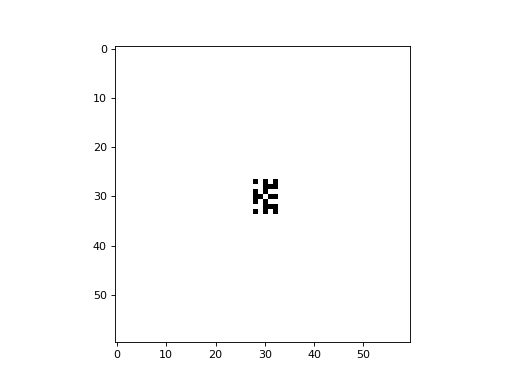
The following is an example of the Fredkin self-replicating CA with a von Neumann neighborhood, implemented with CellPyLib:

import cellpylib as cpl
import numpy as np

cellular_automaton = cpl.init_simple2d(60, 60)
# the letter "E"
cellular_automaton[0][28][28] = 1
cellular_automaton[0][28][29] = 1
cellular_automaton[0][28][30] = 1
cellular_automaton[0][29][28] = 1
cellular_automaton[0][30][28] = 1
cellular_automaton[0][30][29] = 1
cellular_automaton[0][30][30] = 1
cellular_automaton[0][31][28] = 1
cellular_automaton[0][32][28] = 1
cellular_automaton[0][32][29] = 1
cellular_automaton[0][32][30] = 1

def activity_rule(n, c, t):
    current_activity = n[1][1]
    return (np.sum(n) - current_activity) % 2

cellular_automaton = cpl.evolve2d(cellular_automaton, timesteps=20,
                                  apply_rule=activity_rule, neighbourhood="von Neumann")

cpl.plot2d_animate(cellular_automaton, interval=350)

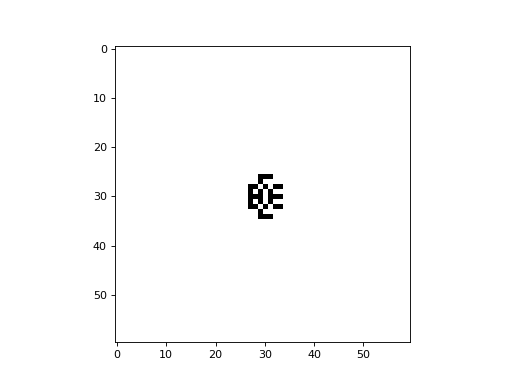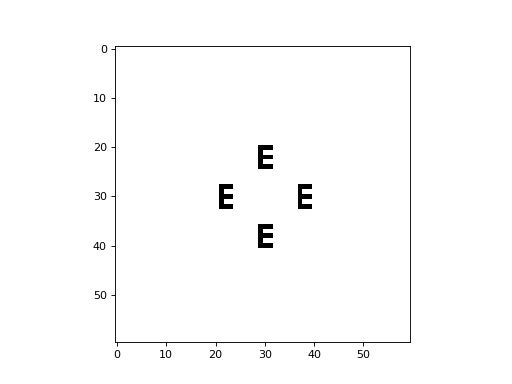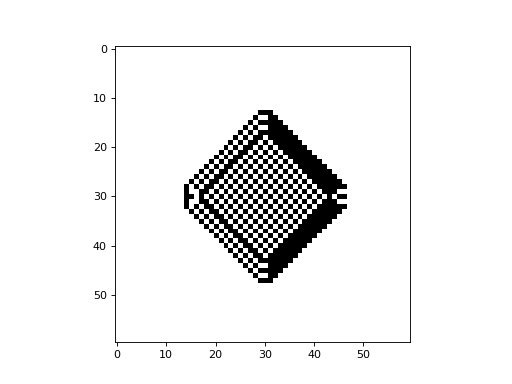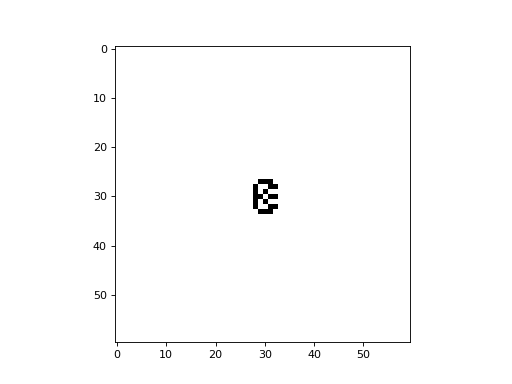
The following is an example of the Fredkin self-replicating CA with a Moore neighborhood, implemented with CellPyLib:

import cellpylib as cpl
import numpy as np

cellular_automaton = cpl.init_simple2d(60, 60)
# the letter "E"
cellular_automaton[0][28][28] = 1
cellular_automaton[0][28][29] = 1
cellular_automaton[0][28][30] = 1
cellular_automaton[0][29][28] = 1
cellular_automaton[0][30][28] = 1
cellular_automaton[0][30][29] = 1
cellular_automaton[0][30][30] = 1
cellular_automaton[0][31][28] = 1
cellular_automaton[0][32][28] = 1
cellular_automaton[0][32][29] = 1
cellular_automaton[0][32][30] = 1

def activity_rule(n, c, t):
    current_activity = n[1][1]
    return (np.sum(n) - current_activity) % 2

cellular_automaton = cpl.evolve2d(cellular_automaton, timesteps=20,
                                  apply_rule=activity_rule, neighbourhood="Moore")

cpl.plot2d_animate(cellular_automaton, interval=350)

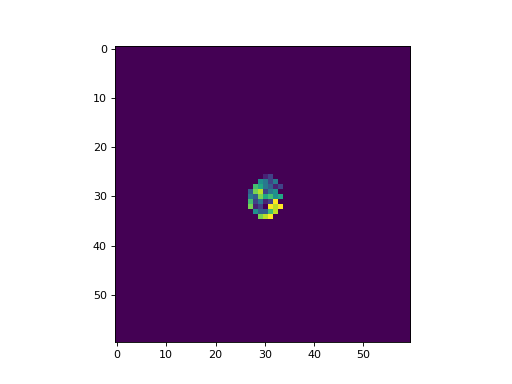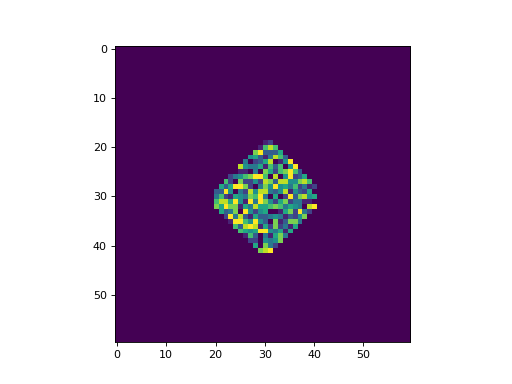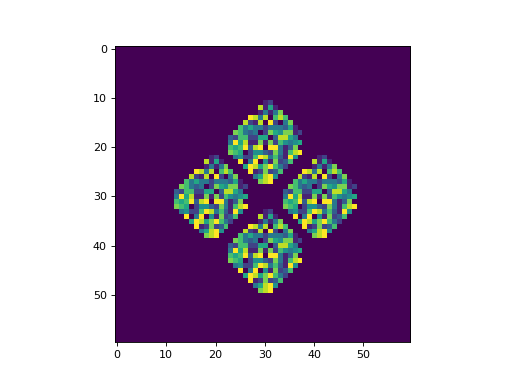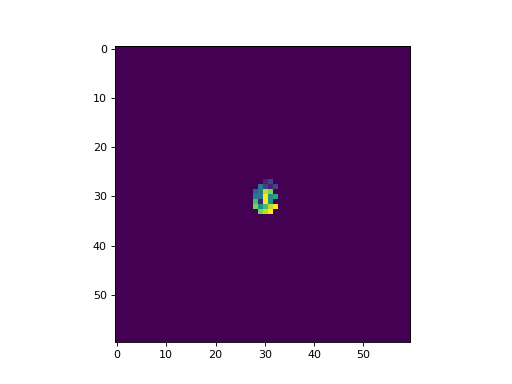
The following is an example of the Fredkin self-replicating multi-color CA with a von Neumann neighborhood, implemented with CellPyLib:

import cellpylib as cpl
import numpy as np

cellular_automaton = cpl.init_simple2d(60, 60)
# the letter "E"
cellular_automaton[0][28][28] = 0
cellular_automaton[0][28][29] = 1
cellular_automaton[0][28][30] = 2
cellular_automaton[0][29][28] = 3
cellular_automaton[0][30][28] = 4
cellular_automaton[0][30][29] = 5
cellular_automaton[0][30][30] = 6
cellular_automaton[0][31][28] = 7
cellular_automaton[0][32][28] = 8
cellular_automaton[0][32][29] = 9
cellular_automaton[0][32][30] = 10

def activity_rule(n, c, t):
    current_activity = n[1][1]
    return (np.sum(n) - current_activity) % 11

cellular_automaton = cpl.evolve2d(cellular_automaton, timesteps=23,
                                  apply_rule=activity_rule, neighbourhood="von Neumann")

cpl.plot2d_animate(cellular_automaton, interval=350, colormap="viridis")

References:

Edwin R. Banks, Information Processing and Transmission in Cellular Automata. MIT dissertation. January 1971.

https://www.johndcook.com/blog/2021/05/03/self-reproducing-cellular-automata/

https://www.johndcook.com/blog/2021/05/03/multicolor-reproducing-ca/