Hopfield Network
The Hopfield Network can be thought of as a cellular automaton where all cells are neighbours of eachother. The cells (or neurons) are binary units, and the activity rule is a simple threshold rule, where the weighted inputs to a cell are summed and compared to a threshold value. The weights are learned from the training data.
CellPyLib includes a built-in implementation of a Hopfield Network, in the
HopfieldNet class, based on the idea that the Hopfield Network can be viewed as a
kind of cellular automaton.
To use it, we must first train the network, by giving it a set of patterns:
import cellpylib as cpl
import numpy as np
hopfield_net = cpl.HopfieldNet(num_cells=35)
zero = [
0, 1, 1, 1, 0,
1, 0, 0, 0, 1,
1, 0, 0, 0, 1,
1, 0, 0, 0, 1,
1, 0, 0, 0, 1,
0, 1, 1, 1, 0,
0, 0, 0, 0, 0]
one = [
0, 1, 1, 0, 0,
0, 0, 1, 0, 0,
0, 0, 1, 0, 0,
0, 0, 1, 0, 0,
0, 0, 1, 0, 0,
0, 0, 1, 0, 0,
0, 0, 0, 0, 0]
two = [
1, 1, 1, 0, 0,
0, 0, 0, 1, 0,
0, 0, 0, 1, 0,
0, 1, 1, 0, 0,
1, 0, 0, 0, 0,
1, 1, 1, 1, 1,
0, 0, 0, 0, 0]
# replace the zeroes with -1 to make these vectors bipolar instead of binary
one = [-1 if x == 0 else x for x in one]
two = [-1 if x == 0 else x for x in two]
zero = [-1 if x == 0 else x for x in zero]
P = [zero, one, two]
hopfield_net.train(P)
As shown above, we must instantiate an instance of a HopfieldNet, specifying the
number of cells. Then, we must call train(), providing a list of training
examples. NOTE: Only Hopfield Networks with an odd number of cells is currently supported due to limitations of the
implementation.
Using the HopfieldNet involves providing a potentially incomplete pattern, and
evolving the network for a pre-specified number of timesteps. The network state should settle into a pattern that
resembles those seen during training. It acts like a content-addressable (associative) memory.
half_two = [
0, 0, 0, 0, 0,
0, 0, 0, 0, 0,
0, 0, 0, 0, 0,
0, 1, 1, 0, 0,
1, 0, 0, 0, 0,
1, 1, 1, 1, 1,
0, 0, 0, 0, 0]
half_two = [-1 if x == 0 else x for x in half_two]
cellular_automaton = np.array([half_two])
cellular_automaton = cpl.evolve(cellular_automaton, timesteps=155,
apply_rule=hopfield_net.apply_rule, r=hopfield_net.r)
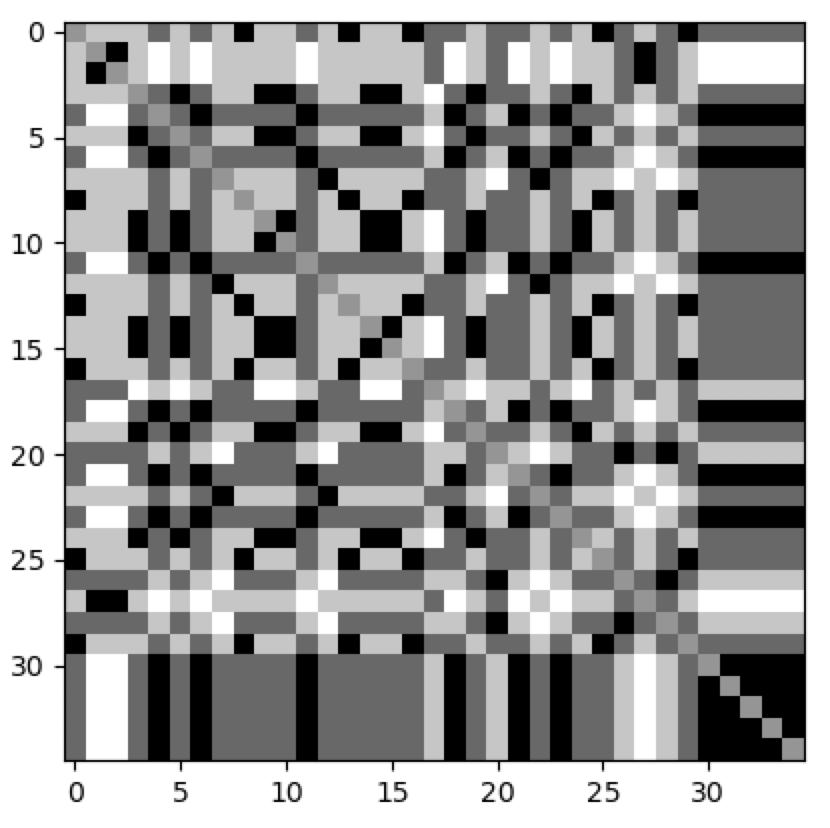
cpl.plot(hopfield_net.W)
cpl.plot2d_animate(np.reshape(cellular_automaton, (155, 7, 5)))

References:
J. J. Hopfield, “Neural networks and physical systems with emergent collective computational abilities”, Proceedings of the National Academy of Sciences of the USA, vol. 79 no. 8 pp. 2554–2558, April 1982.