Conway’s Game of Life

Conway’s Game of Life is a very famous 2D Cellular Automaton. It uses a simple rule to give rise to a complex system that is capable of universal computation, in addition to its ability to entertain and fascinate.

CellPyLib has a built-in function, game_of_life_rule(), that can be used to produce the Game of Life 2D CA:

import cellpylib as cpl

# Glider
cellular_automaton = cpl.init_simple2d(60, 60)
cellular_automaton[:, [28,29,30,30], [30,31,29,31]] = 1

# Blinker
cellular_automaton[:, [40,40,40], [15,16,17]] = 1

# Light Weight Space Ship (LWSS)
cellular_automaton[:, [18,18,19,20,21,21,21,21,20], [45,48,44,44,44,45,46,47,48]] = 1

# evolve the cellular automaton for 60 time steps
cellular_automaton = cpl.evolve2d(cellular_automaton, timesteps=60, neighbourhood='Moore',
                                  apply_rule=cpl.game_of_life_rule, memoize='recursive')

cpl.plot2d_animate(cellular_automaton)
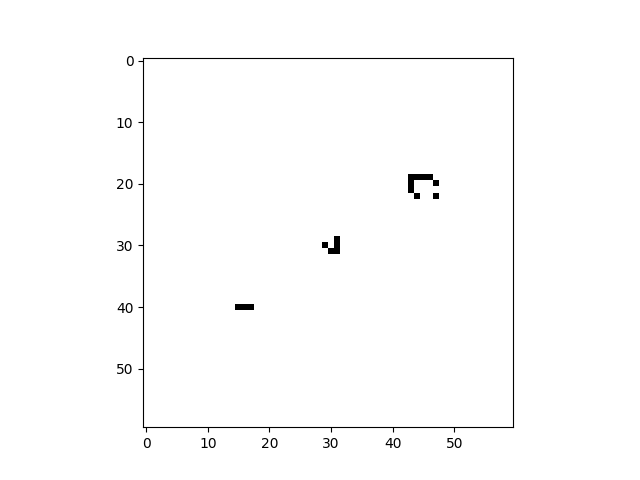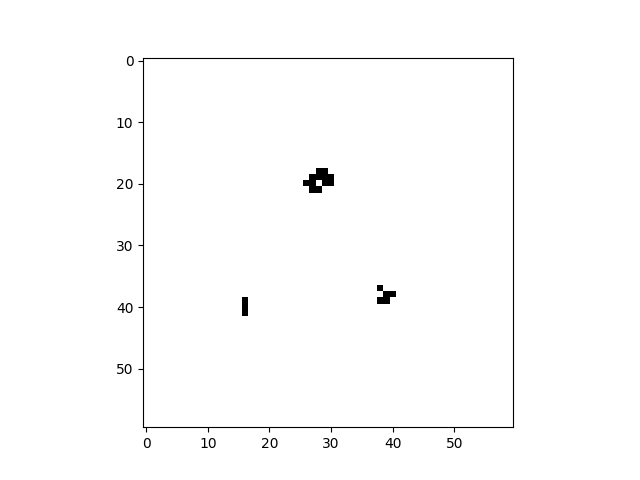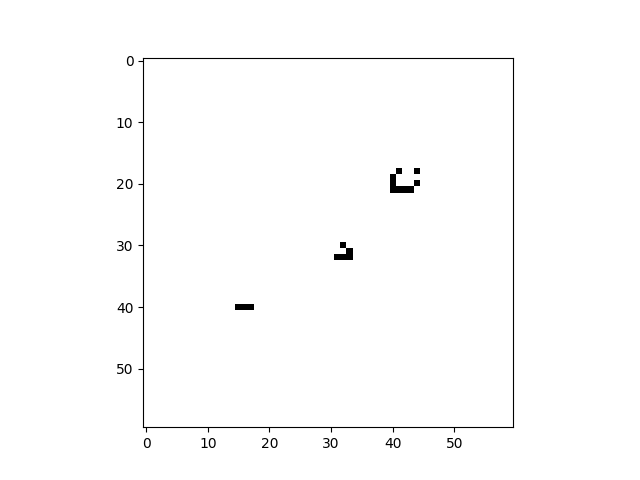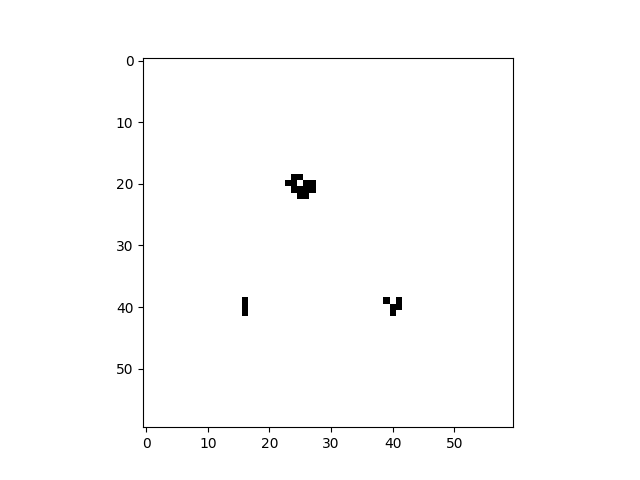
_images/game_of_life.gif

References:

Conway, J. (1970). The game of life. Scientific American, 223(4), 4.